Cite as: Davis, Daniel. 2013. “Modelled on Software Engineering: Flexible Parametric Models in the Practice of Architecture.” PhD dissertation, RMIT University.
2.0 – The Challenges of Parametric Modelling
Neil Leach observes that “many people have misgivings about the term parametric” (Leach and Schumacher 2012). Whilst writing this thesis I contemplated avoiding any controversy by replacing parametric with a less disputed synonym: associative geometry, scripting, flexible modelling, algorithmic design. I would not be the first author to shy away from a term that others, like Patrik Schumacher (2010), have declared “war” over.1 These battles and misgivings surrounding the term parametric are relatively recent. They signify, if nothing else, the growing importance of parametric modelling within the discourse of architecture. For this reason I use the term parametric throughout this thesis – not because I want to go to war, but because the misgivings about the term parametric helps to explain the misgivings of using parametric models.
Owen Hatherley (2010) argues that the debates surrounding parametric modelling stem from a shift in definition. The term parametric was co-opted, says Hatherley (2010), from its provenance in the “digital underground” by “arrivistes” who have jostled to claim the term as their own whilst parametric design ascended towards “mainstream acceptance.” Hatherley cites Schumacher as an example of an arriviste, owing to Schumacher’s (2008) infamous claim that parametric design is a “contemporary architectural style that has achieved pervasive hegemony within the contemporary architectural avant-garde.” Hatherley (2010) goes on to quote my previous articles – where I have argued that parametric design is not defined by an architectural style (Davis 2010) – as “perhaps the nearest proof that there really is an avant-garde [of parametric design] although perhaps Schumacher has little to do with it.” I will make a similar argument in this chapter by showing how the definition of parametric has shifted and, in doing so, obscured many of the challenges associated with parametric modelling.
I begin this chapter by exploring the various definitions of parametric modelling. I argue that there is a propensity to define parametric modelling in terms of the model’s outputs even though the defining feature of a parametric model is not the outputs but rather the need to construct and maintain relationships associated with the model. I go on to explore why architects are attracted to this seemingly unintuitive design process and I investigate the difficulties architects encounter with using parametric models. I argue that these difficulties are not necessarily obvious if parametric modelling is only defined and understood in terms of the model’s outputs. Accordingly, I spend most of this chapter discussing the challenges of defining and using parametric models, both as a way to position my research and as a way to highlight under-represented parts of the discourse that are important in understanding why architects sometimes find parametric modelling challenging.
2.1 – What is Parametric Modelling?

Figure 5: The eleventh page from Robert Woodbury’s (2010) Elements of Parametric Design. Woodbury asks “what is parametric modelling?” but never quite gives the answer.
“What is parametric modelling?” is the title that heads the second chapter in Robert Woodbury’s (2010) book Elements of Parametric Design. Woodbury dedicates twelve pages to the question, but instead of directly answering the question he spends most of these pages explaining the workings of forward-propagating parametric models. Woodbury’s most forthright answer appears on the chapter’s first page (fig. 5): “parametric modelling introduces fundamental change: ‘marks’, that is, parts of the design, relate and change together in a coordinated way” (Woodbury 2010, 11). But Woodbury never pauses to explain how relating marks together differs from the relationships found in a plethora of alternative modelling methods, notably BIM. This is not to chastise Woodbury, for Elements of Parametric Design is one of the seminal books on parametric modelling, but this is to highlight the difficulty even experts have in articulately answering basic questions like what is parametric modelling?
Defining what parametric modelling is and what makes it unique, is an important first step towards identifying the idiosyncratic challenges parametric models present. In the following pages I traverse a range of definitions that various architects have put forward: from the historic definition of parametric, through to the claims that all design is parametric, and that either change, tooling, or parametricism defines parametric. In doing so I make the case that many contemporary definitions tend to privilege what parametric models do (in terms of model behaviour or stylistic outcomes) but that it is how parametric models come to be (through the construction and maintenance of relationships) that distinguishes parametric modelling from other forms of architectural representation.
A Historic Definition
Online version note: In earlier drafts of my thesis this history was much longer (it even had its own chapter at one stage). You can find an earlier and lengthier draft of this section in my previously published blogpost.
The term parametric originates in mathematics but there is debate as to when designers initially began using the word. David Gerber (2007, 73), in his doctoral thesis Parametric Practice, credits Maurice Ruiter for first using the term in a paper from 1988 entitled Parametric Design.2 1988 was also the year Parametric Technology Corporation (founded by mathematician Samuel Geisberg in 1985) released the first commercially successful parametric modelling software, Pro/ENGINEER (Weisberg 2008, 16.5). But Robert Stiles (2006) argues that the real provenance of parametric was a few decades earlier, in the 1940s’ writings of architect Luigi Moretti (Bucci and Mulazzani 2000, 21). Moretti (1971, 207) wrote extensively about “parametric architecture,” which he defines as the study of architecture systems with the goal of “defining the relationships between the dimensions dependent upon the various parameters.” Moretti uses the design of a stadium as an example, explaining how the stadium’s form can derive from nineteen parameters concerning things like viewing angles and the economic cost of concrete (Moretti 1971, 207). Versions of a parametric stadium designed by Moretti (fig. 6) were presented as part of his Parametric Architecture exhibition at the Twelfth Milan Triennial in 1960 (Bucci and Mulazzani 2000, 114). In the five years following the exhibition, between 1960 and 1965, Moretti designed the Watergate Complex, which is “believed to be the first major construction job to make significant use of computers” (Livingston 2002). The Watergate Complex is now better known for the wiretapping scandal that took place there and Moretti is “scarcely discussed” (Stiles 2006, 15) – even by the many architects who today use computers to create parametric models in the manner Moretti helped pioneer.
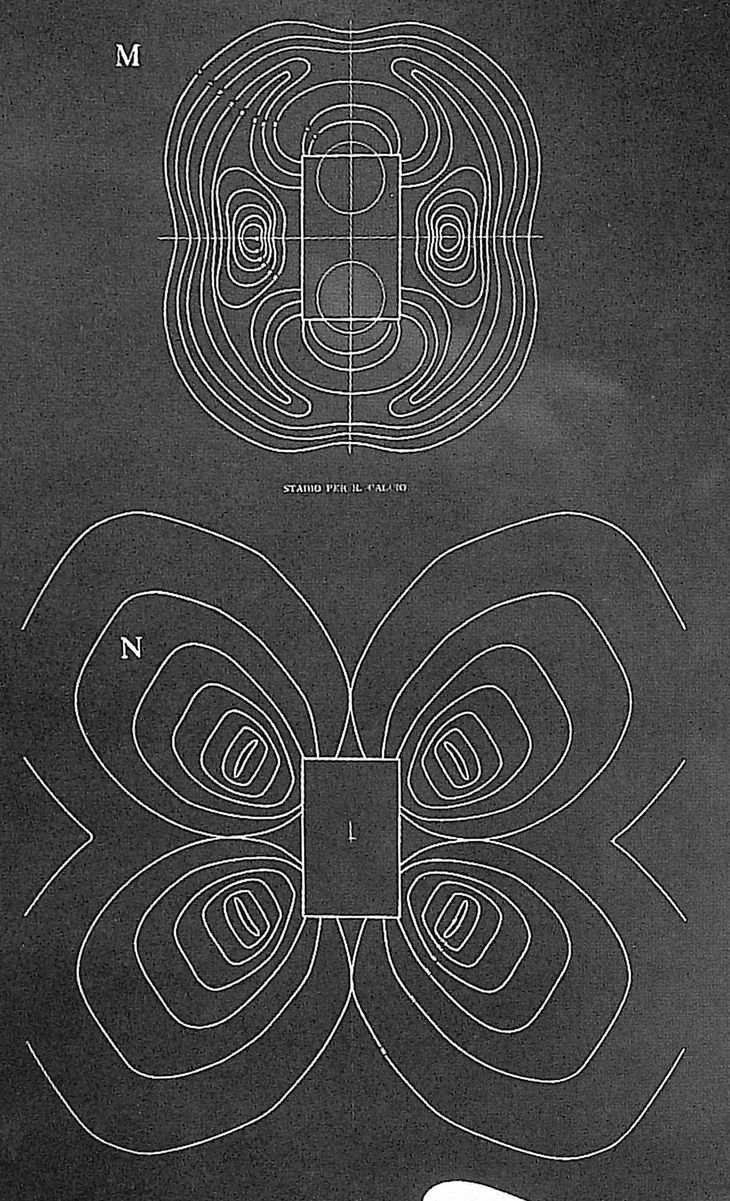
Figure 6: Stadium designs by Luigi Moretti from the 1960 Parametric Architecture exhibition at the Twelfth Milan Triennial. Each stadium derives from a parametric model consisting of nineteen parameters. Top: The plans for stadium version M and N showing the “equi-desirability” curves (Converso and Bonatti 2006, 243) Bottom: A model of stadium N.

A model of stadium N by Luigi Moretti. Exhibited at the 1960 Parametric Architecture exhibition at the Twelfth Milan Triennial. The stadium derives from a parametric model consisting of nineteen parameters.
Moretti did not fear obscurity as much as he feared the incorrect use of mathematical terms like parametric. He wrote to his friend Roisecco that “inaccuracy [regarding mathematical terms] is, in truth, scarier than the ignorance before [when architects knew of neither the terms nor Moretti]” (Moretti 1971, 206). Parametric has a long history in mathematics and the earliest examples I can find of parametric being used to describe three-dimensional models comes almost one hundred years prior to Moretti’s writings. One example is James Dana’s 1837 paper On the Drawing of Figures of Crystals (other examples from the period include: Leslie 1821; Earnshaw 1839).3 In the paper Dana explains the general steps for drawing a range of crystals and provisions for variations using language laced with parameters, variables, and ratios. For instance, in step eighteen Dana tells the reader to inscribe a parametric plane on a prism:
If the plane to be introduced were 4P2 the parametric ratio of which is 4:2:1, we should in the same manner mark off 4 parts of e, 2 of ē and 1 of ë.
Dana 1837, 42
In this quote Dana is describing the parametric relationship between three parameters of the plane (4:2:1) and the respective division of lines e, ē, and ë. The rest of the twenty-page paper possesses similar statements that explain how various parameters filter through long equations to affect the drawing of assorted crystals. Dana’s crystal equations resemble those that would be used by architects 175 years later to develop parametric models of buildings, engendering them with what Moretti (1957, 184) has called (incidentally) a “crystalline splendour.”
Figure 7: Instances of James Dana’s crystal drawings. Above: Setting up the coordinate system (Dana 1837, 41). Below: Impact of changing the edge chamfer ratio (Dana 1837, 43).
Parametric is given no special significance in Dana’s writing. Dana does not describe his drawings as parametric, nor does he claim, as Schumacher (2009a, 15) later would, that designing with parametric equations “justifies the enunciation of a new style in the sense of an epochal phenomenon.” Rather, Dana uses parametric in its original mathematical sense, a word given no more emphasis than other technical terms like parallel, intersection, and plane.
When used by Dana in 1837, or by mathematicians today, parametric signifies what the Concise Encyclopedia of Mathematics calls a “set of equations that express a set of quantities as explicit functions of a number of independent variables, known as ‘parameters’” (Weisstein 2003, 2150).4 This definition sets forth two critical criteria:
- A parametric equation expresses “a set of quantities” with a number of parameters5.
- The outcomes (the set of quantities) are related to the parameters through “explicit functions”6. This is an important point of contention in later definitions since some contemporary architects suggest that correlations constitute parametric relationships.
An example of a parametric equation is the formulae that define a catenary curve:
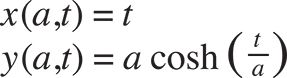
These two formulae meet the criterion of a parametric equation. Firstly, they express a set of quantities (in this case an x quantity and a y quantity) in terms of a number of parameters (a, which controls the shape of the curve; and t, which controls where along the curve the point occurs). Secondly, the outcomes (x & y) are related to the parameters (a & t) through explicit functions (there is no ambiguity in the relationships between these variables). This is the origin of the term parametric: a set of quantities expressed as an explicit function of a number of parameters.
All Design is Parametric
Since Dana’s (1837) parametric crystal drawings 175 years ago, architects have gradually begun using both parametric models and the term parametric.7 Early examples include Antoni Gaudí using a hanging chain model to derive the form of Colònia Güell at the turn of the twentieth-century8 (M. Burry 2011, 231) and Frei Otto similarly using physical parametric models as a form finding technique beginning in the 1950s (Otto and Rasch 1996). Slightly after Moretti held his Parametric Architecture exhibition in 1960 (Bucci and Mulazzani 2000, 114), Ivan Sutherland (1963) created the first parametric software, Sketchpad. However, it was not until Parametric Technology Corporation released Pro/ENGINEER in 1988 that parametric modelling software became commercially viable (Weisberg 2008, 16.10), and it took at least another decade for parametric modelling software to be specifically designed for architects. Today architects craft parametric models in a range of software environments: from history-based modellers9, to visual scripts10, physical modelling11, and textual programming environments12.
While one could argue that architects have spent decades gradually adopting parametric modelling, some have argued that architects have always produced parametric models since all design, by definition, derives from parameters. This claim has been put forward by several authors, including David Gerber in his doctoral thesis on Parametric Practices where he contends:
It must be stated that architectural design is inherently a ‘parametric’ process, and that the architect has always operated in a ‘parametric fashion’.
Gerber 2007, 54
The same argument has been made by Robert Aish and Robert Woodbury:
Parametric modelling is not new: building components have been adapted to context for centuries.
Aish and Woodbury 2005, 152
In a similar vein, Mark Burry rhetorically asks whether the opposite is true, whether non-parametric design exists:
‘Parametric design’ is tantamount to a sine qua non; what exactly is non-parametric design?
M. Burry 2011, 18
Roland Hudson holds a similar opinion and opens his doctoral thesis, Strategies for Parametric Design in Architecture, with the sentence:
This thesis begins with the assertion that all design is parametric.
Hudson 2010, 18
For each of these authors, the claim that ‘all design is parametric’ stems from the observation that all design necessarily involves parameters like budget, site, and material properties. While this is undoubtedly true, the pivotal part of a parametric equation is not the presence of parameters but rather that these parameters relate to outcomes through explicit functions. This explicit connection does not exist for all the parameters involved in a design project. Typically relationships between parameters and outcomes are correlations; the budget has a noticeable affect on the design outcome but normally the mechanism that links the budget to the outcome is – at best – ambiguous. Therefore, by interpreting parametric to mean, literally, design from parameters these authors downplay the importance of explicit relationships to parametric modelling and instead base their definition of parametric upon the observable interface to the model.
Change is Parametric
Another observable characteristic of a parametric model – besides the presence of parameters – is that the geometry changes when the parameters change. This leads some to claim that change is parametric. Chris Yessios, the founder and CEO of the modelling software FormZ, summarises the history of this interpretation:
Initially, a parametric definition was simply a mathematical formula that required values to be substituted for a few parameters in order to generate variations from within a family of entities. Today it is used to imply that the entity once generated can easily be changed.
Yessios 2003, 263
Yessios (2003, 263) acknowledges the mathematical origins of parametric modelling but also advances a definition couched in behavioural terms: the trademark behaviour of a parametric model being that it “can easily be changed.” Robert Woodbury (2010, 7) seems to advance a similar definition, beginning Elements of Parametric Design with the two sentences: “Design is change. Parametric modelling represents change.” This is followed shortly thereafter with the claim, “parametric modelling introduces fundamental change: ‘marks’, that is, parts of the design, relate and change together in a coordinated way” (Woodbury 2010, 11).13 Robert Aish (2011, 23) has similarly emphasised the importance of variation by saying a parametric model “directly exposes the abstract idea of geometric ‘transformation’.” Revit Technology Corporation14 used a similar definition in a greeting to visitors of the Revit website:
Para.me.tric adj. Math. A quantity or constant whose value varies with the circumstances of its application, as the radius line of a group of concentric circles, which [sic] varies with the circle under consideration.
Revit Technology Corporation 2000b (emphasis theirs)
While Revit Technology Corporation claim that their definition comes from mathematics, the definition in no way resembles the actual mathematical definitions I cited earlier. Critically, their definition overlooks the role of explicit functions in a parametric model, an oversight also present in the various definitions given by Woodbury, Aish, and Yessios. In place of explicit functions are notions that parametric models can be defined by the variation they produce. Change is an easily identifiable characteristic of a parametric model and one that many authors choose to define parametric modelling by.
Defining parametric modelling in terms of change conjures Heraclitus’s dictum ‘Nothing endures but change’. Although parametric models change, so too does practically everything else in the world, except perhaps change itself. Even explicit geometric models can commonly be changed through rotation, or scaling, or moving a mesh vertex. And more specialised representations, like BIM, are set up to ensure changes to the underlying database also change the associated models. Thus, while parametric models change, and while parametric models are celebrated for being able to change, change is hardly a unique feature of parametric modelling. By saying parametric modelling is change, the various authors once again focus on what parametric models do, without considering the unique qualities of how parametric models are created.
Tooling is Parametric
Mark Burry (2011, 8) begins Scripting Cultures by saying, “we are moving rapidly from an era of being aspiring expert users to one of being adept digital toolmakers.” Many other prominent authors describe themselves as toolmakers and claim that parametric models are a type of drawing tool (examples in key books and doctoral theses include: Aranda and Lasch 2005; M. Burry 2011; Fischer 2008; Gerber 2007; Hudson 2010; Kilian 2006; Woodbury 2010; Shelden 2002). This toolmaking analogy has been in use since at least 1983 when the then co-founder of Autodesk, John Walker (1983), made the heady charge that their actions over the coming year “will decide whether AutoCAD becomes synonymous with ‘drawing tool’.” In doing so Walker attempted to position AutoCAD alongside analogue drawing tools like the tee-square and the drafting table, a task he and his competitors were largely successful at. In recent years, the term has been further catalysed by Benjamin Aranda and Chris Lasch’s book Tooling where they explain seven basic parametric recipes for what they call drawing tools.
Whether tooling is an appropriate descriptor for what architects do is a question I will leave for the discussion at the end of this thesis. For now I would like to pause and consider how tooling implies an answer to the question what is parametric modelling?
The term tooling conveys a separation between maker and user; between the nameless person who makes a tee-square and the designer that uses the tool. Aranda and Lasch (2005, 9) reinforce this division, concluding the introduction to Tooling by saying, “once this field [meaning the tool] is defined as a flexible and open space, the job of designing begins.” Aish (2001, 23) similarly divides the act of creating a tool and the job of designing when he remarks: “Software developers do not design buildings. Their role is to design the tools that other creative designers, architects and engineers use to design buildings.” The implied division between tool use and tool making is significant: it suggests the creation and the use of a parametric model is temporally separated, and perhaps even organisationally separated.
The implications of this separation are eloquently (if unintentionally) captured by Roland Hudson (2010) in his thesis Strategies for Parametric Design in Architecture. Hudson (2010) draws upon many of the same authors quoted in this chapter, dividing them within his literature review under the headings “creating the model” and “exploring the design space” (fig. 8). This division continues as Hudson discusses six case studies of projects employing parametric models, talking about each parametric model exclusively under the heading “overview of the completed model,” as if creating the parametric model is separate and less relevant than using the model. Hudson (2010, 230-45) then concludes his research by saying that parametric model creation and design investigation are two separate activities. Hudson (2010, 245) says that a person using a parametric model to design ends up “refining parameter values, problem descriptions and the structure of the parametric model rather than suggesting substantial changes”. Given the categorical division underlying Hudson’s research, it is hard to see how he could conclude anything else; a researcher is not going to see substantial changes if they only look at “overviews of the completed model”.

Figure 8: A selection from the contents of Roland Hudson’s (2010) thesis Strategies for Parametric Design in Architecture. Hudson’s distinction between creating and using a parametric model comes through in his thesis structure: the literature review is split between alternating headings of “creating the model” and “exploring the design space”; and each case study evaluation focuses on the “overview of the completed model” often without discussing any aspect of the model’s creation.

Hudson’s reasoning is not abnormal. Definitions presented earlier – that all design is parametric or that change is parametric – show how designers can become fixated on what ‘completed’ parametric models do, often leaving out details of how parametric models are created or changed. This bias can create the impression of a separation between a parametric model’s creation and use; a separation that privileges design exploration through parameter manipulation and underplays the possibility of ongoing model development; a separation that leads Hudson and many others to say tooling is parametric.
Parametricism is Parametric
When Owen Hatherley (2010) talks about arrivistes repurposing the term parametric, Hatherley is really talking about Patrik Schumacher (director of Zaha Hadid Architects). Parametric was adopted by Schumacher as a call to arms in his newly declared “style war” (2010) first presented as a “parametricist manifesto” (2008) based upon “parametric paradigma” (2008) and dubbed “Parametricism” (2008) at 11th Venice Architecture Biennale. Since then, the polemic has been refined and republished in countless locations, always generating much discussion.
Parametricism is a knowingly provocative notion, claiming “post-modernism and deconstructivism were mere transitional episodes” (Schumacher 2010, 43) and that parametric design will be “the great new style after modernism” (2010, 43). Schumacher (2009a, 16) identifies parametricism with a set of “negative heuristics” like “avoid rigid geometric primitives” and “avoid juxtaposition.” He counterbalances this with a set of “positive heuristics” including “consider all forms to be parametrically malleable” and “differentiate gradually (at varying rates)” (Schumacher 2009a, 16).
Schumacher (2009b) illustrates his parametricism heuristics almost exclusively with Zaha Hadid projects. When I pressed Schumacher on his lack references to other projects, Schumacher – who holds a PhD in philosophy – said “I am a practicing architect before I am a theorist” (Davis 2010). By this Schumacher does not mean that he constructs parametric models as practicing architect. Schumacher never writes about using a parametric model and I can find no evidence that Schumacher creates parametric models at Zaha Hadid. Rather, Schumacher’s practice largely consists of reviewing what other architects have produced with parametric models. Considering Schumacher’s perspective, it is somewhat understandable that he would say “the emergence of a new epochal style … is more important than methodological and procedural innovations via specific computational techniques” (Leach and Schumacher 2012). After all, it is the stylistic outputs that Schumacher sees, not the methodology or procedure. In this sense Schumacher is not too far removed from the many other theorists who also define parametric modelling in terms of what the model does. In answering the question what is parametric modelling? parametricism represents an extreme position, and a position many architects like to distance themselves from, yet it is a position many others come close to in their outcome focused definitions of parametric modelling.
Modelling versus Design
In contrast to Schumacher, my thesis focuses on the methodological and procedural innovations required for parametric modelling instead of focusing on enunciating the emergence of a new epochal style of parametric design. The discourse surrounding parametric design (whether parametric design is taken as a verb to describe the process of designing with a parametric model, or as a noun to describe the outcomes of this process) seems unlikely to reach a resolution in the near future, nor does it need to. I will leave it for others to debate how parametric design fits into the broader culture of architecture; for now there is a pressing need to understand the technological challenges presented by parametric models. Finding ways to make a parametric model more flexible may have ramifications in terms of architectural design but the immediate ramifications will be for the multitudes of architects currently using parametric models in their practice. Thus, my research focuses almost entirely on parametric modelling and leaves aside the debates surrounding the design implications.
What is a Parametric Model?
The definition of a parametric model, like a parametric model itself, has an unsettled variability. At any particular time parametric may signify all of design, or only the designs that change, or tooling, or design in the style of parametricism. This collective disagreement exists even on an individual level, with many prominent authors providing different definitions across the span of their work (in the proceeding pages, I have often been able to quote the same author under different definitions of parametric). Unsurprisingly, architects like Patrik Schumacher have seized this confusion as an opportunity claim the meaning of parametric, whilst others have distanced themselves from the term altogether. At SIAL15 for instance, parametric models are often referred to as flexible models (M. Burry 2011, 105), which is a description that emphasises – like most definitions of parametric – what the models do rather than how the models were created.
The creation of the parametric model distinguishes it from other forms of architectural representation. Returning to the Concise Encyclopedia of Mathematics, a parametric equation is defined as a “set of equations that express a set of quantities as explicit functions of a number of independent variables, known as ‘parameters’” (Weisstein 2003, 2150). The mathematical definition can be refined by recognising that the “set of quantities” in the context of design representation is typically geometry (although not always). Thus, a parametric model can be defined as: a set of equations that express a geometric model as explicit functions of a number of parameters. This is the intended meaning when nineteenth-century scientists and mathematicians like James Dana (1837) refer to parts of their geometric drawings as parametric. This is what mathematician Samuel Geisberg (Teresko 1993, 28) meant when he founded Parametric Technology Corporation and created the first commercially successful parametric software. This is the definition used by Fabian Scheurer and Hanno Stehling (2011, 75) as well as Ipek Dino (2012, 208-10). And when Woodbury (2010, 11-22) describes the mechanics of a forward propagating parametric model in his chapter “What is Parametric Modelling?” the model he describes conforms to this definition. Therefore, a parametric model is unique, not because it has parameters (all design, by definition, has parameters), not because it changes (other design representations change), not because it is a tool or a style of architecture, a parametric model is unique not for what it does but rather for how it was created. A parametric model is created by a designer explicitly stating how outcomes derive from a set of parameters.
The explicit connection between parameters and the geometric model potentially excludes a number of model types. Dino (2012, 209) has argued linguistic algorithms (such as shape grammars) and biological algorithms (such as genetic algorithms, flocking, and cellular automata) tend not to be parametric because they lack explicit connections. While these algorithms may contain parameters, their parameters work like a budget in a brief; they undoubtably influence the outcome but there is no explicit connection between a specific parameter and a specific outcome. Yet the boundary between parametric and non-parametric is not clear cut. For instance, Sketchpad (Sutherland 1963, 110-19) has two solving methods: the one-pass method, which analytically solves the explicit functions (Sutherland 1963, 118-19); and the relaxation method, which bypasses the explicit functions through numeric optimisation. Sketchpad seamlessly switches between the two solving methods and to an end user they both appear parametric even though one relies upon explicit functions while the other does not. Other fringe cases include BIM models where changes to data may trigger a set of functions that recalculate a series of models. Even explicit geometry has some parametric characteristics. For instance, the endpoint of a line could be thought of as a parameter to a set of functions that transform the line. While I am aware of these grey areas, for the remainder of this thesis I will be discussing models that are unambiguously parametric – models where the designer has defined the explicit connections between parameters and the geometry. In the next section I consider why a designer would want to do so.
2.2 – Why Use a Parametric Model?
If you were to ask an architect to describe a medium for designing architecture, one that fosters creativity and exploration, they would probably not reply ‘a set of equations that express a geometric model as explicit functions of a number of parameters’. Yet explicit functions and parameters are the medium of choice for the many architects who design with parametric models. Understanding why architects choose to use parametric models – a seemingly counterintuitive medium for creativity and exploration – is a crucial step towards understanding the challenges associated with parametric modelling.
Thinking Parametrically
Expressing design intentions with parameters and explicit functions requires a different way of thinking than most designers are accustomed to. In addition to thinking about what they are designing, architects working with parametric models must also think about the logical sequence of formulas, parameters, and relationships that explain how to create their designs (Aish 2005, 12; Woodbury 2010 24-25). Some dub this parametric thinking or algorithmic thinking. Learning to think parametrically is “a hard-won skill, not acquired with ease” say all but one of forty experts interviewed by Mark Burry (2011, 38). Although learning to design in such a mediated manner can be difficult, the logical precision can also be enjoyable for designers who relish pushing back against imposed constraints, and for designers who like how parametric modelling forces them to explicitly state (and therefore consider) every geometric relationship (Aish 2005, 12; M. Burry 2011, 38-39; Kilian 2006, 300-03; Woodbury 2010 24-25). However, the real benefit of learning to think parametrically comes from the cost of design changes.
The Cost of Change
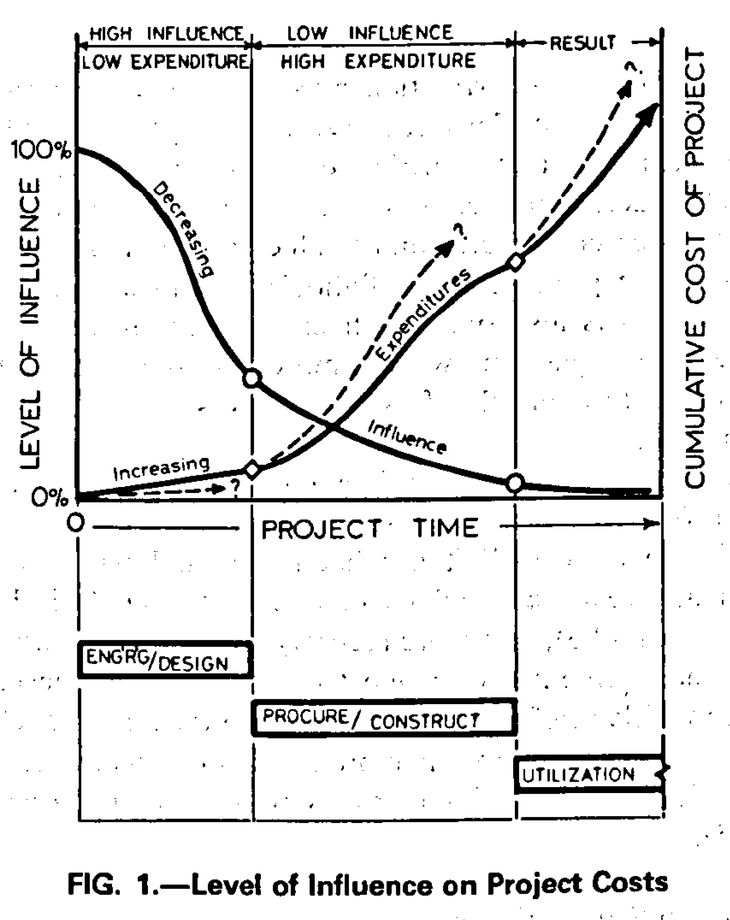
Figure 9: Paulson’s curve (1976, 588). In the text accompanying this graph, Paulson talks about the benefits of making early decisions when the designer’s level of influence is high.
In 1976 Boyd Paulson sketched a graph (fig. 9) showing that a designer’s level of influence over an architecture project decreases as the project progresses. Paulson (1976, 588) points out that the first decision a designer faces on any project – whether to commence the project or not – has total influence over the project’s future. He goes on to argue that all subsequent decisions have a diminishing influence and are generally more costly to implement. In other words: as designs become more developed, they also become more difficult to change. Paulson published his observations in a few construction management textbooks (Barrie and Paulson 1991) but the idea never became widely circulated.
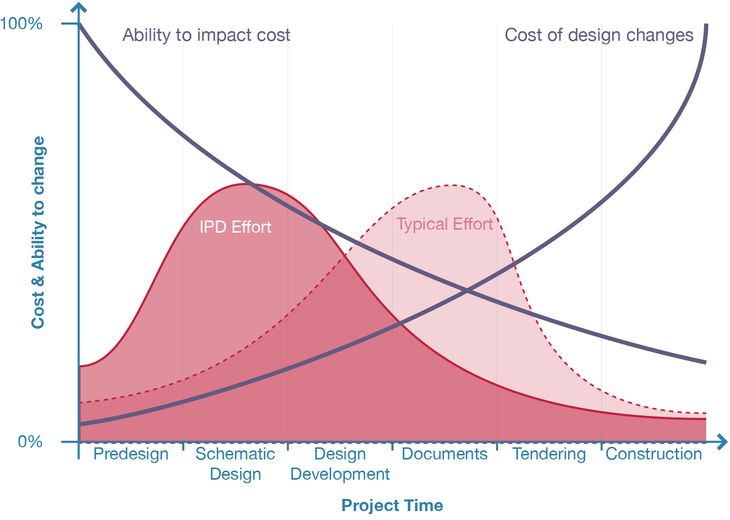
Figure 10: MacLeamy’s curve (2001). MacLeamy advocates taking the typical design effort and shifting it to an earlier stage of the project. In theory this means that designers are working when their decisions have the most impact and least associated cost.
Paulson’s graph reappeared in May 2001 at a resort in Mexico. The leaders from HOK (one of the world’s largest architecture firms) had gathered at the resort to discuss “key strategies for the future” (HOK 2012). During the discussions, Patrick MacLeamy presented a graph (fig. 10) showing that a designer has the most “ability to impact [a project’s] cost and functional capabilities” (MacLeamy 2010) at the start a project, and that this ability decreases during a project while the cost of making design changes increases. The graph MacLeamy presented was identical to Paulson’s. MacLeamy claimed the work as his own (perhaps unaware of Paulson’s efforts) and HOK went on to promote Paulson’s graph under the name MacLeamy’s curve (HOK 2012) – a name that has stuck thanks in part to HOK’s marketing clout.16 Two years after MacLeamy presented the graph to the leaders of HOK, MacLeamy was appointed CEO, a position he has held for almost a decade (HOK 2012).
As CEO of HOK and the international chair of buildingSMART17, MacLeamy has used his curve to champion the front-loading of architecture projects. MacLeamy (2010) advocates making design decisions early in the project (shifting the design effort forward) since his curve shows that design changes are less costly to make at the start of the project compared to the end. Paulson (1976, 591-92) drew the same conclusions from his graph and suggested construction knowledge should be injected earlier in the design process. More sophisticated examples of front-loading are given by MacLeamy (2010) who advocates both of the following: Integrated Project Delivery (IPD), which contractually amalgamates all the project parties to guide the design team towards viable solutions early in the project; and BIM, which provides a central project database to improve communication between team-members while also aiding early stage simulations and later stage project documentation. These ideas have been widely disseminated and MacLeamy’s conception of front-loading has informed contemporary architectural practice in everything from the American Institute of Architects (AIA 2007, 21-31) guidelines for IPD to the instruction manuals for Autodesk’s Revit (Read, Vandezande, and Krygiel 2012, fig. 5.7).
Discussing the cost of change may make some designers uncomfortable, particularly if they perceive their costly changes as valuable contributions to a project. However, cost in this context is a measure of the designer’s capacity to make change; the designer’s ability to design. Ostensibly, front-loading should empower designers by encouraging them to act when the cost of change is low and their capacity to make change is high. Yet, the paradox of front-loading is that by forcing design decisions early in the project, the project becomes more developed and therefore, according to MacLeamy’s curve, more costly to change later on. It is this increase in the cost of change that should make designers uncomfortable because it signals a reduction in the designer’s capacity to make late changes.
The introduction of parametric modelling was motivated by a desire to decrease the cost of change. This motivation is discussed by Samuel Geisberg, the founder of Parametric Technology Corporation, during an interview with Industry Week in 1993:
The goal is to create a system that would be flexible enough to encourage the engineer to easily consider a variety of designs. And the cost of making design changes ought to be as close to zero as possible. In addition, the traditional CAD/CAM software of the time unrealistically restricted low-cost changes to only the very front end of the design-engineering process.
Geisberg quoted in: Teresko 1993, 28
Geisberg’s comments suggest that instead of looking at MacLeamy’s cost of change curve and concluding design efforts should be shifted to the “very front end of the design-engineering process,” a better conclusion may be to shift the cost of change curve so that the “cost of making design changes [is] as close to zero as possible.” In theory, a parametric model helps lower the cost of change provided the model’s parameters and explicit functions require less effort to change than alternative modelling methods. Geisberg calls this flexibility (Teresko 1993, 28). In chapter 4 I discuss the various nuances of flexibility, but for now flexibility can be understood as a measure of the cost of design changes and, by proxy, a component of the designer’s capacity to design.
Flexibility makes-up the central tenet of parametric modelling. By maintaining a flexible model the designer can afford to make changes, which is important given the inevitability of change on an architecture project. While some changes can be anticipated and perhaps even front-loaded, many changes come from forces outside the designer’s sphere of influence. For instance, the client can change the brief, politicians can change the legislation, and market forces can change the price of materials. Other changes occur because design is a knowledge generating process. Often it is only through iteration, exploration, and reflection that the problem – much less the design response – becomes known (Glegg 1969; Schön 1983; Lawson 2005; Cross 2006). In the face of these inevitable changes, the flexibility of a parametric model’s parameters and explicit functions makes for an alluring design medium; one many architects employ to help improve the designer’s capacity to design.
2.3 – Reported Difficulties with Models in Practice
While the flexibility of a parametric model purportedly helps designers accommodate change, there is growing evidence that this is not always the case. “Many times,” writes Rick Smith (2007, 2), architects working with parametric models are finding they have to “start all over again” once changes incapacitate their models. Parametric Technology Corporation (PTC 2008, 1) admit “this situation is fairly common” with users often finding that they spend “too much time re-creating designs, or can’t respond to unexpected changes fast enough, or [that their] design cycles are actually taking longer [compared to using a non-parametric model]” (2008, 1). A similar sentiment is expressed by the authors quoted at the very start of this thesis (Gerber 2007, 205; J. Burry 2007, 622; Holzer et al. 2007, 639; Aish and Woodbury 2005, 151; M. Burry 1996, 78). In the following section I revisit what these authors say about the practice of parametric modelling and investigate the associated challenges they reveal.
Evidence of Challenges
Very few architects have spoken publicly about how they construct and maintain their parametric models; fewer still in a critical manner. This is not entirely surprising considering the relatively recent adoption of parametric modelling by most architects. Only in the past decade have the challenges of computational power, workflows, and algorithms receded to the point where parametric modelling has gone from an issue largely of theory to the subject of practice.
When architects do write about the practice parametric modelling there is a tendency to understate the challenges. As Thomas Fischer (2008, 245) laments, firsthand accounts of “failures and dead-ends … seem to be rare and overshadowed by the great number of post-rationalised, outcome-focused reports on digital design toolmaking.” This observation ties into the point made earlier in this chapter: architects are inclined to focus more on what parametric models do than how the models come to be. From this perspective, the failures and dead-ends can be hard to see. But through the veneer of architects talking positively about the outcomes of projects they were personally involved in, there are fragments containing frank admissions of the problems encountered. The handful of authors who have written candidly about these challenges make up the bibliography of this section.
The most explicit critique of parametric modelling comes in a short, six-page paper entitled Technical Notes from experiences and studies in using Parametric and BIM architectural software (Smith 2007). The paper is not peer reviewed, has not been published, and lists only one source. Ordinarily such a paper could be dismissed as misattributed opinion, only, this paper is written by Rick Smith.
Rick Smith played a large part in introducing parametric modelling to the architecture industry. Smith began working as a CAD technician for Lockheed in 1979 (Smith 2010), well before most architecture firms had computers. By the start of the 1990s, Smith was designing parts for the United States space shuttle with Dassault Systèmes’ CATIA (Smith 2010). Based on Smith’s experience in the aerospace industry, Frank Gehry and Associates hired Smith in 1991 to help design the Barcelona Fish using CATIA – one of the first times software of this calibre was used in the architecture industry. Smith ended up spending a decade consulting to Gehry, employing parametric modelling on some of Gehry’s most prominent projects, such as the Guggenheim Bilbao (1993-97), the Experience Music Project (1995-00), and the Walt Disney Concert Hall (1992-03). The success of this collaboration helped spawn the sister company Gehry Technology (incorporated in 2001), which went on to develop the parametric modelling software Digital Project (2004) – a modified version of CATIA intended for architects. Given the decades Smith has spent helping pioneer parametric modelling in the architecture industry, it is very significant for him to now turn around and highlight the flaws.
Since 2007 Smith has announced the challenges associated with parametric modelling in the short, six-page white-paper prominently displayed on the website of his consultancy, Virtual Build Technologies. The white-paper identifies five major shortcomings with parametric modelling (Smith 2007, 2):
- Parametric models require a degree of front-loading.
- Anticipating flexibility can be difficult.
- Major changes break parametric models.
- Changes can be hard to see visually.
- Reusing and sharing models is problematic.
Smith’s points seem to resonate with what other authors have written, even if they do not write so emphatically. In the following section I take in turn each of Smiths five critiques and consider whether evidence from peer-reviewed authors corroborates his self-published opinions.
One: Front-loading
When you model using parametrics you are programming following similar logic and procedural steps as you would in software programming. You first have to conceptualize what it is you’re going to model in advance and its logic. You then program, debug and test all the possible ramifications where the parametric program might fail. In doing so you may over constrain or find that you need to adjust the program or begin programming all over again because you have taken the wrong approach.
Smith 2007, 2
In Smith’s first critique of parametric modelling, he points out that creating a parametric model requires some degree of upfront planning. This is reiterated by Weisberg (2008, 16.12) who recalls that even in 1993 designers creating parametric models in Pro/ENGINEER needed to “carefully plan the design, defining ahead of time which major elements would be dependent upon other elements.” Planning is a necessary component of parametric modelling because the logical rigidity of a model’s explicit functions requires that the designer anticipate, to some degree, the parameters of the model and the hierarchy of dependencies between functions. This “prerationalization process is often found to be arduous,” states Gerber (2007, 205), “as it requires a significant amount of upfront cognitive investment.” While pre-rationalisation can be onerous, the real difficulty of pre-rationalisation is not the upfront cognitive investment but rather the risk that the designer may invest time on “the wrong approach” (Smith 2007, 2). As Axel Kilian (2006, 54) warns, “structuring the design approach early on in the design process … offers little flexibility once a model has been created.” This is a similar problem to MacLeamy’s front-loading: many changes in an architecture project cannot be anticipated upfront, and decisions made too early in the project may raise the subsequent cost of design changes since any major change will undo all of the initial work. Aish and Woodbury (2005, 151) echo this statement by acknowledging “parameterization may require additional effort, may increase complexity of local design decisions and increase the number of items to which attention must be paid in task completion.” The additional effort required to design using explicit functions necessitates that designers have some notion of the design outcome prior to modelling. This upfront planning can be challenging, particularly in a process as notoriously hard to anticipate as the design process.
Two: Anticipating Flexibility
Once you think you have a working parametric model you may still find you haven’t programmed a parameter of the geometry in a way that is adjustable to a designer’s future request. A designer might say I want to move and twist this wall, but you did not foresee that move and there is no parameter to accommodate the change. It then unravels your program. Many times you will have to start all over again. Imagine trying to do this on a complex and fully integrated building.
Smith 2007, 2
Part of the upfront planning of a parametric model, according to Smith’s second critique, involves anticipating future design changes. If changes can be anticipated, the model can be structured with the appropriate parameters to accommodate these changes. However, if a change is not anticipated, the designer must accommodate the change by modifying the model’s explicit functions. This process of “conceiving, arranging and editing dependencies is the key parametric task” according to Woodbury (2010, 25). As with the task of initially building the parametric model, modifying the explicit functions can be challenging, particularly on a “complex and fully integrated building” (Smith 2007, 2). A critical endeavour of the designer is therefore to avoid unnecessarily rebuilding the model by anticipating future changes and creating parametric models with the flexibility to accommodate these anticipated changes from the start.
Given the importance of anticipating flexibility, a seemingly obvious response is to make every aspect of a model flexible; add parameters for every possible whimsy of the designer. But parameters come at a cost. They require work upfront to implement, and they require even more work to change. This investment may not pay off if the parameter is rarely used. Therefore, the skill of anticipating flexibility is getting the balance right between too much and too little flexibility. Fabian Scheurer and Hanno Stehling share this sentiment:
The challenge of building a parametric model is to untangle the interdependencies created by different requirements and find a set of rules that is as simple as possible while remaining flexible enough to accommodate every occurring case. In other words: to pinpoint the view to the exact level of abstraction where no important point is lost and no one gets distracted by unnecessary detail.
Scheurer and Stehling 2011, 75
Thus, an ideal parametric model encompasses all the variations the designer wants to explore with the most concise set of parameters possible. According to Jane Burry and Mark Burry (2006, 793) this catches designers in a paradox: upfront they need to anticipate potential changes to the model, yet they lack the knowledge to do so because it is the “very variability of the model that uncovers potential ranges of [new] possibilities that leads to design explorations.” The paradox of anticipating flexibility presents a challenge for designers, one they must overcome to avoid making major model changes.
Three: Major Changes
After all the time and effort of programming the geometry to where you think you have it right, you may find you still have to start all over again because the initial design concept has completely changed.
Smith 2007, 2
Smith’s third critique of parametric modelling is that major changes will break even the most flexible parametric models. Ordinarily changes can be accommodated either through modifying parameters or by modifying the model’s explicit functions. However, an industry survey by the Aberdeen Group (2007, i) of more than 150 firms (8% of which were architecture firms) found that designers “often end up spending more time fixing models than if they had simply started from scratch.” Weisberg (2008, 16.12) noted similar behaviour in his observations of engineers, concluding the difficulty of modifying a parametric model’s explicit functions was such that “in extreme cases (and sometimes in cases that were not particularly that extreme), the user was forced to totally recreate the model.” In reality the designer is never forced since a designer always has the option of not making a particular change. Although, admittedly, there is little comfort in being asked to choose between either completely rebuilding your parametric model or compromising your design intentions to fit the limitations of an existing parametric model.
Architects tend to be unwilling to talk about the “failures and dead-ends” (Fischer 2008, 245) that result in models being rebuilt. When they do, it is often only in passing. For instance, David Gerber (2007, 205) mentions that if the “topology of a project changes the [parametric] model generally needs to be remade.” Yet apart from this single sentence, Gerber does not dedicate any more space in his five hundred-page thesis to the fact that models employed for their flexibility apparently fail if the topology of the project changes – a seemingly critical detail for a thesis entitled Parametric Practices. Slightly more depth can be found in various exposés of the parametric modelling process. For example, Mark Burry (1996, 78) speaks to the issue of topological fragility when discussing the design process for the triforium column of the Sagrada Família. Burry initially built the parametric model from hyperbolic paraboloid geometry but, during the subsequent design process, the design team decided to test whether the column could instead be made from conoid geometry. When Burry (1996, 78) tried to make this topological transformation, he found himself in a situation where “there is no solution other than to completely disassemble the model and restart at the critical decision.” These struggles with topological transformations, particularly ones that result in models being rebuilt, are especially acute for architects given the relative lack of topological consistency in building forms when compared to the typically homeomorphic forms of boats, planes, and cars dealt with in other industries.
While topological transformations can be difficult, they are not the only type of major change that causes models to be rebuilt. Dominik Holzer et al. (2007) tells of how unanticipated changes can completely disrupt a model, as happened on the model for AAMI Park stadium in Melbourne. Holzer joined the project as a member of ARUP’s team assisting with the structural calculations during the design development. By this stage of the design process, many parts of the project were finalised and therefore included as invariable geometry in the model. It was expected that the design would become more resolved during the design development process, however, the opposite happened: “the number of variable design factors increased” (Holzer et al. 2007, 637). As more and more of the original design intent was changed, and as the changes impacted parts of the model initially assumed to be invariable, the changes became of “such a disruptive nature that the parametric model schema could not cope with them” and the “model consequently fell apart” (Holzer et al. 2007, 639). Holzer had no choice but to rebuild the model. Changing a parametric model is often so disruptive that Hudson (2010, 240) recommends “early models should be treated as disposable and not precious.” Jane Burry (2007, 622) also notes that it is commonplace when parametric modelling to “return to the metaphorical drawing board to edit the relational graph or remodel completely.” While Weisberg (2008, 16.12) observes designers trying to avoid this by “planning their design work in order to avoid having to start over if major changes were made to the design.” However, even with the best front-loaded anticipation of changes, the inflexibility of parametric models in the face of major changes often present the designer with only one viable option: start over.
There will always be changes outside the designer’s control – to the legislation, budget, and the client’s favourite colour. And since designers learn through designing, there will always be changes that cannot be anticipated prior to modelling. These changes are ordinarily accommodated by modifying parameters or by modifying the model’s explicit functions. However, if the change is large enough, or the topology unfamiliar enough, this choice will diminish to just one option: rebuild the model. A decidedly inflexible outcome.
Four: Change Blindness
Once you have your program working if anyone changes a parameter it could affect the geometry somewhere in the design that you didn’t want to be changed. This occurs often and the change may not be detected until much later in the design phase, or even worse, in the more expensive construction phase.
Smith 2007, 2
Designers often fail to observe changes in models, says Smith in his fourth critique of parametric modelling. His claim is corroborated by strong empirical evidence from numerous psychologists. Summarising this existing research, Simons and Levin (1997, 261) note, “experiments using a diverse range of methods and displays have produced strikingly similar results: unless a change to a visual scene produces a localizable change or transient at a specific position on the retina, generally, people will not detect it.” This phenomenon is known as change blindness. A study by Nasirova et al. (2011) of twenty participants using parametric models found “change blindness did indeed occur … making change detection for 3D parametric [modelling] highly challenging, slow and confusing” (2011, 762; a similar point is made in: Erhan, Woodbury, and Salmasi 2009). A designer suffering from change blindness will essentially be unable to see certain model changes, even though the changes are unobscured on screen while the designer actively looks for them. On occasion the designer will fail to see any changes at all. Phillips (1974) demonstrates that this problem is exacerbated by the latency between seeing one variation and seeing the other variation (which, in a parametric model, is the time between making a change and seeing the result). The propensity of designers to suffer from change blindness has two major implications for the application of parametric modelling:
- Firstly, as Rich Smith warned, changes to a parametric model may have undetected consequences. In chapter 7 I discuss a project where inadvertent changes went undetected until they caused near catastrophic problems during the construction phase.
- Secondly, if a designer is unable to identify what has changed between two model variations, then they may struggle to make an informed evaluation of design changes.
Five: Reuse and Sharing
This also points to the fact that any operator using the model needs intimate knowledge of the parametric program that is written for that specific design. This logic knowledge is not easily transferred with the 3D model. In a sense the original programmer of the model then becomes the owner of the model. Many times if the program is too complex the original programmer is the only one who can work with it.
Smith 2007, 2
Smith’s final critique of parametric modelling is that parametric models are difficult to reuse and share. Parametric Technology Corporation (PTC 2008, 3) acknowledge this problem and say “even after a model is created, other designers can’t easily modify the design because they don’t possess the knowledge about how it was created and the original design intent.” Yanni Loukissas (2009) observes that because parametric models are difficult to share, one architect within an organisation inevitably becomes the “keeper of the geometry” – the person responsible for the parametric model by virtu of being the only person capable of modifying the model. A similar conclusion was drawn by the Aberdeen Group’s survey (2007, 3), which identified the following “top four challenges to design reuse” (2007, 3):
- Model modification requires expert CAD knowledge.
- Models are inflexible and fail after changes.
- Users cannot find models to reuse.
- Only the original designer can change models successfully.
The first, second, and fourth item on this list are singled out by the Aberdeen Group (2007, 3) “as testament to the fact that feature based models [a synonym for parametric models] can be a barrier to design reuse.” In many ways, these three points are just manifestations of Smith’s third critique: major changes often break parametric models. After all, if a designer breaks their own model trying to implement a change, then a designer unfamiliar with the model is going to be in a far worse position to adapt that model to a totally new circumstance. Research by Kolarić et al. (2010) indicates that even simple tasks becomes cognitively demanding when a parametric model is unfamiliar. Identifying a relationship in a parametric model containing twelve objects took participants on average ten seconds to complete, and they were wrong 20% of the time (even though they had a 50% chance of randomly answering the yes/no question correctly; Kolarić et al. 2010, 709-10). This is to say nothing of the difficulty of identifying relationships in a much larger model or the difficulty of modifying relationships once they are correctly found – two tasks necessary for reuse and sharing.
The Challenges of Parametric Modelling
Rick Smith’s five critiques of parametric modelling are a subject absent from much of the architectural discourse. However, dispersed through the writings of architectural theorists, practicing architects, software manufacturers, and psychologists are pieces of evidence that strongly support Smith’s five claims. Collating this fragmented evidence represents a significant furthering in our understanding of parametric modelling. Perhaps most notably, it demonstrates that parametric models used in practice are often blindsided by the very thing they purportedly accommodate: change.
Smith’s first three critiques (front-loading, anticipating flexibility, and major changes breaking models) are really manifestations of the same thing: the difficulty of expressing unsettled design intentions with explicit functions. Given this difficulty, front-loading is frequently necessary to orchestrate a parametric model’s explicit functions into an appropriate hierarchy. Once in this hierarchy, the difficulty of changing the relationships often prompts designers to try – somewhat in vain – to avoid changes by anticipating them first. This is a situation that unfortunately shifts the rhetoric around parametric modelling, from one of designers embracing change, to one of designers eschewing change. To a lesser extent, the challenges of working with explicit functions also contribute to the problems with sharing models, since being unfamiliar with a model only exacerbates the difficulties of changing the model. The only critique from Smith not directly linked to fragility of explicit functions is change blindness, which instead arises from difficulties all humans have in visually observing and evaluating change.
Smith’s critiques show that architects are clearly facing challenges with expressing design intentions using explicit functions, while also struggling to observe design changes and to reuse models. These observations are substantiated independent of the parametric modelling software used, the design team composition, the stage parametric modelling is used in a project, the types of changes asked for, and the design complexity. While each of these circumstances may be singled out as a problem, Smith’s critiques suggest that they are symptoms, or at least aggravations, of problems common to all parametric models. These are problems largely concerning explicit functions but they are not solely technological, they concern the designer and they also concern the inherent unpredictability of the design process. Smith’s critiques indicate that designers are often finding themselves in situations where they cannot modify the model’s explicit functions and the designer is left with two undesirable choices: they can delay the project and rebuild the model, or they can avoid making the change altogether.
2.4 – Conclusion
The difficulties of parametric modelling are set in motion by the struggles to define it. The term parametric originates in mathematics where, since at least the 1830s, mathematicians and scientists have used the term in relation to various geometric representations. However, as architects have adopted parametric modelling as a design medium, the definition of parametric has become muddied. Now when architects use the term parametric, they could mean all of design, or only the designs that change, or tooling, or design in the style of parametricism. The disagreement exists even on an individual level, with many prominent authors defining parametric differently across the span of their work.
The commonality of these contended definitions is that they focus on what parametric models do. To a certain extent this makes sense: it is, after all, what parametric models do that makes them interesting to architects. For architects, parametric models purportedly improve the designer’s ability to make changes, thereby improving their capacity to design. In theory a designer can modify a model’s parameters and see the design change almost instantly. As such, parametric models have come to be understood in terms of their outputs; a method for producing tools, or making parametricism, or creating design representations that change in relation to parameters. This focus on what parametric models do suggests a separation between creating and doing, a separation that underplays the significance of creating and maintaining a parametric model.
It is the construction and maintenance of the explicit relationships inside a parametric model that distinguishes parametric modelling from other forms of design representation. As such, I define a parametric model as many mathematicians would: as a set of equations that express a geometric model as explicit functions of a number of parameters. While arriving at this definition has been a contribution of this chapter, the primary contribution of this chapter has been to expose the difficulties associated with using explicit functions to design. Learning to express uncertain design outcomes with the computational logic of explicit functions is, for most architects, a “hard-won skill” (M. Burry 2011, 38). Even for experienced practitioners, like Rick Smith, the networks of explicit functions they weave often become so brittle that starting over is easier than making a change. Flexible parametric models often turn out to be inflexible in practice, and models set up to embrace change often instead end up restricting change. For architects, these difficulties are largely without precedent since parametric modelling is often “more similar to programming than to conventional design” (Wesiberg 2008, 16:12). The difficulties are familiar, however, to many software engineers who also often struggle to create flexible code – as I will detail in the following chapter.
Thesis Navigation
- Return to table of contents
- Goto previous chapter
- Goto next chapter
- Download entire thesis as PDF (30mb)
Footnotes
1:Neil Leach claims that, as a result of the misgivings around the term parametric, “few people in the West working at the forefront of computation use the term parametric or parametricism, although it is still popular in China for some reason” (Leach and Schumacher 2012).
2:Gerber claims Ruiter’s paper was published in Advances in Computer Graphics III (1988). When I looked at this book, none of the papers were titled Parametric Design and none of the papers were written by Ruiter (he was the editor not writer). As best I can tell, there never was a paper titled Parametric Design produced in 1988. The first reference I can find to Ruiter’s supposed paper is in the bibliography of Javier Monedero’s 1997 paper, Parametric Design: A Review and Some Experiences. It is unclear why Monedero included the seemingly incorrect citation since he never made reference to it in the text of his paper. As an aside: the word parametric does appear four times in Advances in Computer Graphics III – on pages 34, 218, 224, & 269 – which indicates that the use of parametric in relation to design was not novel at the time.
3:By searching for parametric in Google Ngrams (http://books.google.com/ngrams/) I was able to find the earliest occurrences of parametric from the collection of books that Google has scanned. While James Dana (1837) is one of the more compelling results, other examples include: Samuel Earnshaw (1839, 102), who wrote about “hyperbolic parametric surfaces” deformed by lines of force in a paper that gave rise to Earnshaw’s theorem; and Sir John Leslie (1821, 390), who proved the self-similarity of catenary curves using “parametric circles” in his book on geometric analysis. Google has scanned only a limited collection of books so there may be even earlier examples that were not returned in these searches. Nevertheless, Dana’s writings in 1837 significantly predate any claims I have found in various histories of parametric design as to the first use of the term parametric in relation to drawing.
4:This definition is consistent with definitions in other mathematical dictionaries and encyclopedias. I have chosen to cite from the Concise Encyclopedia of Mathematics as the editor, Eric Weisstein (who is also the chief editor of Wolfram Mathworld) is considered an authoritative source.
5:Parameter can have a number of meanings, even when used by mathematicians. The grammarian James Kilpatrick (1984, 211-12) quotes a letter he received from R. E. Shipley: “With no apparent rationale, nor even a hint of reasonable extension of its use in mathematics, parameter has been manifestly bastardized, or worse yet, wordnapped into having meanings of consideration, factor, variable, influence, interaction, amount, measurement, quantity, quality, property, cause, effect, modification, alteration, computation etc., etc. The word has come to be endowed with ‘multi-ambiguous non-specificity’.” In the Concise Encyclopedia of Mathematics (Weisstein 2003, 2150), the term parameter used in the context of a parametric equation means an “independent variable.” That is, a variable whose value does not depend on any other part of the equation (the prefix para- being Greek for beside or subsidiary).
6:An explicit function is a function whose output value is given explicitly in terms of independent variables. For example, the equation x_∙_x + y_∙_y = 1 is the implicit function for a circle. The function is implicit since the outputs (x and y) are defined in terms of one another. To make the function explicit, x and y have been defined in terms of an independent variable. Thus, the explicit function of a circle becomes: x = cos(t), y = sin(t). By a similar token, saying that ‘x is roughly twice as large as t’ is not an explicit function since there is ambiguity regarding the exact relationship between the variables t and x (the relationship is non-explicit).
7:I have elected not to write a complete history of parametric modelling since doing so would not contribute significantly to the argument developed in the remainder of this thesis. For those interested, I recommend Weisberg’s (2008) detailed account of early CAD software and Gerber’s (2007) chapter on precedents to parametric practice.
8:A hanging chain has at least four parameters: its length, its weight, and the two points it is attached to. Left to hang under the force of gravity, the chain makes a curved shape. This curve is an explicit function of the chain’s parameters with the added property that when inverted the curve stands in pure compression. While there is no computer, the hanging chain is a parametric model due to the presence of parameters that control a shape derived from an explicit function (in this case calculated by gravity).
9:History-based modellers track how the designer creates geometry, allowing the designer to make changes later. Examples include: CATIA, SolidWorks, and Pro/Engineer.
10:Visual scripts resemble flowcharts explaining how parameters generate geometry. Designers can manipulate the script’s inputs or the script itself to change the model. Examples include: Grasshopper, GenerativeComponents, and Houdini.
11:Physical models like Gaudí’s hanging chain model and Frei Otto’s soap films use physical properties to calculate forms based on a set of parameters.
12:There are scripting interfaces included with most CAD programs. These allow designers to setup parameters and a set of explicit functions that generate geometry and other parametric outputs.
13:Woodbury’s definition nods to Sutherland’s (1963, 22) explanation of Sketchpad’s behaviour, “change of a model’s critical part will automatically result in appropriate changes to related parts.” Of course, Sutherland was not explaining the meaning of parametric but rather explaining Sketchpad to an audience who had never seen a person interact with a computer.
14:Revit Technology Corporation was founded by former employees of Parametric Technology Corporation. Their initial ambition was to create the “first parametric building modeler for architects and building design professionals” (RTC 2000a) although since their acquisition by Autodesk in 2002 they have begun branding what they do as Building Information Modelling (BIM).
15:The Spatial Information Architecture Laboratory (SIAL) is a research unit within the Royal Melbourne Institute of Technology (RMIT). My PhD is part of SIAL’s project Challenging the Flexibility of the Inflexible Digital Model – a title that deliberately uses flexible model instead of parametric model.
16:I am extremely grateful to Noel Carpenter for drawing my attention to Paulson’s work in a comment Carpenter left on a blogpost I wrote about MacLeamy (Davis 2011a). As best I can tell, no previous research has cited Paulson when discussing MacLeamy’s curve.
17:BuildingSMART is an influential consortium of CAD manufacturers and users that develops open standards for describing buildings. They are perhaps best known for the development of the IFC standard, which facilitates interoperability in between BIM software.
Bibliography
AIA (The American Institute of Architects). 2007. “Integrated Project Delivery : A Guide.” Accessed 21 November 2012. http://info.aia.org/SiteObjects/files/IPD_Guide_2007.pdf.
Aberdeen Group. 2007. “The Design Reuse Benchmark Report: Seizing the Opportunity to Shorten Product Development.” February. Boston: Aberdeen Group.
Aish, Robert, and Robert Woodbury. 2005. “Multi-level Interaction in Parametric Design.” In Smart Graphics: 5th International Symposium, edited by Andreas Butz, Brian Fisher, Antonio Krüger, and Patrick Olivier, 151–162. Frauenwörth Cloister: Springer.
Aish, Robert. 2005. “From Intuition to Precision.” In 23rd eCAADe Conference Proceedings, 62–63. Lisbon: Technical University of Lisbon.
Aish, Robert. 2011. “Designing at t + n.” Architectural Design 81 (6): 20–27.
Aranda, Benjamin, and Chris Lasch. 2005. Tooling: Pamphlet Architecture 27. New York: Princeton Architectural Press.
Barrie, Donald, and Boyd Paulson. 1991. Professional Construction Management: Including C.M., Design-construct, and General Contracting. Third edition. Hightstown: McGraw Hill.
Bucci, Federico, and Marco Mulazzani. 2000. Luigi Moretti: Works and Writings. New York: Princeton Architectural Press.
Burry, Jane, and Mark Burry. 2006. “Sharing Hidden Power: Communicating Latency in Digital Models.” In Communicating Space(s): 24th eCAADe Conference Proceedings. Volos: University of Thessaly.
Burry, Jane. 2007. “Mindful Spaces: Computational Geometry and the Conceptual Spaces in which Designers Operate.” International Journal of Architectural Computing 5 (4): 611-624.
Burry, Mark. 1996. “Parametric Design and the Sagrada Família.” Architectural Research Quarterly, no. 1 : 70-80.
Burry, Mark. 2011. Scripting Cultures. Chichester: Wiley.
Converso, Stefano, and Fabrizio Bonatti. 2006. “Parametric Model for Architectural Design.” In Game Set and Match: On Computer Games, Advanced Geometries, and Digital Technologies, edited by Kas Oosterhuis and Lukas Feireiss, 242–247. Rotterdam: Episode Publishers.
Cross, Nigel. 2006. Designerly Ways of Knowing. London: Springer-Verlag.
Dana, James. 1837. “On the Drawing of Figures of Crystals.” The American Journal of Science and Arts 32: 30-50.
Davis, Daniel. 2010. “Patrik Schumacher – Parametricism.” Digital Morphogenesis. Published 25 September. /patrik-schumacher-parametricism/.
Davis, Daniel. 2011a. “The MacLeamy Curve.” Digital Morphogenesis. Published 15 October. /macleamy/.
Dino, Ipek. 2012. “Creative Design Exploration by Parametric Generative Systems in Architecture.” METU Journal of Faculty of Architecture 29 (1): 207–224.
Earnshaw, Samuel. 1839. “On the Nature of the Molecular Forces which Regulate the Constitution of the Luminiferous Ether.” Transactions of the Cambridge Philosophical Society 7: 97-112.
Erhan, Halil, Robert Woodbury, and Nahal Salmasi. 2009. “Visual Sensitivity Analysis of Parametric Design Models: Improving Agility in Design.” In Joining Languages, Cultures and Visions: Proceedings of the 13th International Conference on Computer Aided Architectural Design Futures, edited by Temy Tidafi and Tomás Dorta, 815–829. Montreal: Les Presses de l'Université de Montréal.
Fischer, Thomas. 2008. “Designing (tools (for designing (tools for …)))).” PhD dissertation, Royal Melbourne Institute of Technology.
Gerber, David. 2007. “Parametric Practices: Models for Design Exploration in Architecture.” PhD dissertation, Harvard University.
Glegg, Gordon. 1969. The Design of Design. Cambridge: Cambridge University Press.
HOK. 2012. “HOK History + Lore.” Accessed 21 November 2012. http://www.hok.com/lore/.
Hatherley, Owen. 2010. “Zaha Hadid Architects and the Neoliberal Avant-Garde.” MUTE. First published 26 October. http://www.metamute.org/editorial/articles/zaha-hadid-architects-and-neoliberal-avant-garde. Subsequently published in 2011, MUTE 3 (1): 39-53. This print edition does not contain the paragraph cited. Hatherley was unaware of this change (per. comm. 15 August 2011). The online edition was later updated to match the print edition, although the paragraph remains in translations of the article, such as: 2011. “Zaha Hadid y la Vanguadia Neoliberal.” Tintank. Published 15 January. http://www.tintank.es/?p=736
Holzer, Dominik, Richard Hough, and Mark Burry. 2007. “Parametric Design and Structural Optimisation for Early Design Exploration.” International Journal of Architectural Computing 5 (4): 625-644.
Hudson, Roland. 2010. “Strategies for Parametric Design in Architecture: An Application of Practice Led Research.” PhD dissertation, University of Bath.
Kilian, Axel. 2006. “Design Exploration through Bidirectional Modeling of Constraints.” PhD dissertation, Massachusetts Institute of Technology.
Kilpatrick, James. 1984. The Writer’s Art. Kansas City: Andrews, McMeel, and Parker.
Kolarić, Siniša, Halil Erhan, Robert Woodbury, and Bernhard Riecke. 2010. “Comprehending Parametric CAD Models: An Evaluation of Two Graphical User Interfaces.” In Extending Boundaries: Proceedings of the 6th Nordic Conference on Human-Computer Interaction, edited by Ann Blandford, Jan Gulliksen, Ebba Hvannberg, Marta Larusdottir, Effie Law, and Hannes Vilhjalmsson, 707–710. New York: Association for Computing Machinery.
Lawson, Bryan. 2005. How Designers Think: The Design Process Demystified. Fourth edition. Oxford: Elsevier. First published 1980.
Leach, Neil, and Patrik Schumacher. 2012. “On Parametricism: A Dialogue Between Neil Leach and Patrik Schumacher.” Accessed 16 November 2012. http://www.patrikschumacher.com/Texts/On%20Parametricism%20-%20A%20Dialogue%20between%20Neil%20Leach%20and%20Patrik%20Schumacher.html. Originally published in Time + Architecture no. 2012/5: 1–8.
Leslie, John. 1821. Geometrical Analysis and Geometry of Curve Lines. Second edition. Edinburgh: W. & C. Tait.
Livingston, Mike. 2002. “Watergate: The name that branded more than a building.” Washington Business Journal, 17 June.
Loukissas, Yanni. 2009. “Keepers of the Geometry.” In Simulation and Its Discontents, edited by Sherry Turkle, 153–70. Massachusetts: MIT Press.
MacLeamy, Patrick. 2010. “Bim-Bam-Boom! How to Build Greener, High-performance Buildings.” HOK Renew. Accessed 21 November 2012. http://hokrenew.com/2010/02/09/bim-bam-boom-how-to-guarantee-greener-high-performance-buildings/.
Monedero, Javier. 1997. “Parametric Design. A Review and Some Experiences.” In Challenges of the Future: 15th eCAADe Conference Proceedings, edited by Bob Martens, Helena Linzer, and Andreas Voigt. Vienna: Österreichischer Kunstund Kulturverlag.
Moretti, Luigi. 1957. “Forma Come Structtura.” Spazio June-July. Republished in: Federico Bucci and Marco Mulazzani. 2000. Luigi Moretti: Works and Writings. New York: Princeton Architectural Press. Citations refer to the 2000 publication.
Moretti, Luigi. 1971. “Ricerca Matematica in Architettura e Urbanisticâ.” Moebius IV no. 1, 30-53. Republished in: Federico Bucci and Marco Mulazzani. 2000. Luigi Moretti: Works and Writings. New York: Princeton Architectural Press. Citations refer to the 2000 publication.
Nasirova, Diliara, Halil Erhan, Andy Huang, Robert Woodbury, and Bernhard Riecke. 2011. “Change Detection in 3D Parametric Systems: Human-Centered Interfaces for Change Visualization.” In Designing Together: Proceedings of the 14th International Conference on Computer Aided Architectural Design Futures, edited by Pierre Leclercq, Ann Heylighen, and Geneviève Martin, 751–764. Liège: Les Éditions de l’Université de Liège.
Otto, Frei, and Bodo Rasch. 1996. Finding Form: Towards an Architecture of the Minimal. Stuttgart: Axel Menges.
PTC (Parametric Technology Corporation). 2008. “Explicit Modeling: What To Do When Your 3D CAD Productivity Isn’t What You Expected.” White-paper. Needham: Parametric Technology Corporation.
Paulson, Boyd. 1976. “Designing to Reduce Construction Costs.” Journal of the Construction Division 102 (4): 587–592.
Phillips, W. 1974. “On the Distinction Between Sensory Storage and Short-term Visual Memory.” Perception and Psychophysics 16 (2): 283–290.
RTC (Revit Technology Corporation). 2000a. “Revit Technology Corporation Launches Industry’s First Parametric Building Modeler.” Press release, 5 April. Waltham.
RTC (Revit Technology Corporation). 2000b. “Revit Technology Corporation ‑ Product.” http://revit.com/cornerstone/index.html. Copy archived 10 May 2000. http://web.archive.org/web/20000510111053/http://revit.com/cornerstone/index.html.
Read, Phil, James Vandezande, and Eddy Krygiel. 2012. Mastering Autodesk Revit Architecture 2013. Indianapolis: Wiley.
Ruiter, Maurice, ed. 1988. Advances in ComputerGraphics III. Berlin: Springer-Verlag.
Scheurer, Fabian, and Hanno Stehling. 2011. “Lost in Parameter Space ?” Architectural Design 81 (4): 70-79.
Schumacher, Patrik. 2008. “Parametricism as Style: Parametricist Manifesto.” Paper presented at The Darkside Club, 11th Architecture Biennale, Venice, 11 September. Digital copy of text, accessed 17 November 2012. [http://www.patrikschumacher.com/Texts/Parametricism as Style.htm](http://www.patrikschumacher.com/Texts/Parametricism as Style.htm).
Schumacher, Patrik. 2009a. “Parametricism: A New Global Style for Architecture and Urban Design.” Architectural Design 79 (4): 14–23.
Schumacher, Patrik. 2009b. “Parametricism.” Keynote presentation at Intensive Fields, University of Southern California, Los Angeles. Digital video of presentation, accessed 17 November 2012. http://www.patrikschumacher.com/Videos/vid_01_intensive.html.
Schumacher, Patrik. 2010. “The Parametricist Epoch: Let the Style Wars Begin.” Architects’ Journal 231 (16): 41-45.
Schön, Donald. 1983. The Reflective Practitioner: How Professionals Think in Action. London: Maurice Temple Smith.
Shelden, Dennis. 2002. “Digital Surface Representation and the Constructibility of Gehry’s Architecture.” PhD dissertation, Massachusetts Institute of Technology.
Simons, Daniel, and Daniel Levin. 1997. “Change Blindness.” Trends in Cognitive Sciences 1 (7): 261–267.
Smith, Rick. 2007. “Technical Notes From Experiences and Studies in Using Parametric and BIM Architectural Software.” Published 4 March. http://www.vbtllc.com/images/VBTTechnicalNotes.pdf.
Smith, Rick. 2010. “About Virtual Build Technologies.” Accessed 19 November 2012. http://www.vbtllc.com/index_about.html.
Stiles, Robert. 2006. “Aggregation Strategies.” Masters dissertation, University of Bath.
Sutherland, Ivan. 1963. “Sketchpad: A Man-Machine Graphical Communication System.” PhD dissertation, Massachusetts Institute of Technology.
Teresko, John. 1993. “Parametric Technology Corp.: Changing the way Products are Designed.” Industry Week, 20 December.
Walker, John. 1983. “Information Letter #10.” Internal memo at Autodesk Inc. 25 October. Subsequently published as part of John Walker ed. 1994, The Autodesk File: Bits of History, Words of Experience, Fourth edition, Self published with earlier editions published in 1989 by New Riders Publishing.
Weisberg, David. 2008. “The Engineering Design Revolution: The People, Companies and Computer Systems that Changed Forever the Practice of Engineering.” Accessed 23 July 2011. http://www.cadhistory.net.
Weisstein, Eric. 2003. CRC Concise Encyclopedia of Mathematics. Second edition. Boca Raton: Chapman & Hall/CRC.
Woodbury, Robert. 2010. Elements of Parametric Design. Abingdon: Routledge.
Yessios, Chris. 2003. “Is There More to Come?” In Architecture in the Digital Age: Design and Manufacturing, edited by Branko Kolarevic, 259–68. New York: Spon Press.
Illustration Credits
- Figure 5 – Robert Woodbury 2010, 11
- Figure 6 – Federico Bucci and Marco Mulazzani 2000, 114
- Figure 7 – James Dana 1837, 41 & 43
- Figure 8 – Roland Hudson 2010, 5 & 9
- Figure 9 – Boyd Paulson 1976, 588
- Figure 10 – Daniel Davis

Daniel KA
Hi Daniel
I was hoping, you could help me out here.
In the following blog post; Loomis, Mark (Jan 10, 2011). "Rhino Grasshopper VS Generative Components" (Blog). Designplaygrounds. Retrieved Feb 9, 2011. (http://designplaygrounds.com/deviants/rhino-grasshopper-vs-generative-components/)
the GenerativeComponents software is presented as using scripting language rather than using visual scripting (as opposed to your thesis).
Please enlighten me!
Cheers
Daniel
Hi Daniel,
It depends on which version of Generative Components you are talking about. The early versions were a hybrid of visual and textual programming -- relationships were displayed in a symbolic graph but the relationships were created through code. In the later versions of Generative Components (after the Mark Loomis article), Bentley adopted more of a visual programming paradigm: http://www.bentley.com/NR/rdonlyres/716C17AF-E102-4843-90A8-963020F6953D/0/GCVisualProgramming.JPG
Daniel