This is part two of a series on advanced design strategies for Grasshopper definitions. Part one looked at using design patterns to structure definitions and this part will investigate ways to optimise Grasshopper definitions. While it is written for Grasshopper, the ideas are equally applicable to other parametric modelling tools.
Why and when to optimise Grasshopper
In general optimising Grasshopper is a waste of time; the optimisation will take longer than any time you gain from using it. You spend far longer constructing Grasshopper definitions compared to using them so I would favor any change that makes a definition optimally readable over a change that makes a definition computationally optimal. However, in certain cases computational optimisation may be justified, particularly when dealing with real time transformations of models. A little optimization might kick a definition from unusably sluggish to fluid.
In general optimisation should only occur once the definition is fully functional - to avoid optimising a part of the definition that is either not used in the final definition or optimising the wrong part. Once you have the fully functional definition, you can choose the correct part to optimise by measuring how long processes take using the Grasshopper profiling tool.
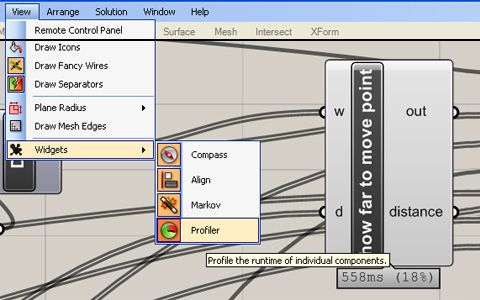
Profile is under the view menu, and draws little boxes under each node with the time it takes to calculate.
Despite its three-digit accuracy, the tool is only approximate, so do not take it as gospel. You will want to focus your optimisation efforts on the areas that are taking the longest time and therefore offer the most reward for optimising. The following is a list of ways to optimise your definition, starting with the most basic and working into the advanced stuff.
Break the model up / Use the place holder pattern
This one is pretty obvious but I have included it for completeness. The general idea is to break a large calculation into more manageable parts. One way to do this is to look for moments in the definition where the graph narrows to one node. For example you might have a function that gives generates the lines for a set of columns and these lines are then fed into a function that generates the columns. You could calculate the lines separately and then in another definition import the lines to generate the columns. Another way to do this is to right click a node and either disable the calculations or turn off the preview. Yet another way to do this is to use the place holder design pattern where you replace complex geometry with temporary and simple geometry. So you might replace columns with a simple pipe and once all the pipes are in the right place, draw the detailed model in place of this pipe.
Simplify curves
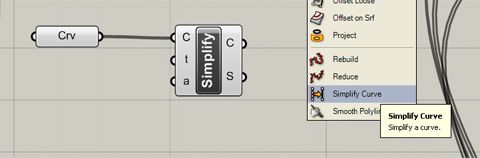
Simplify is under Curve>Util
Simplify curves rebuilds the curve with less control points. This can significantly increase the speed of calculations with these curves, and any objects derived from the curves – like lofts and pipes.
Don’t repeat yourself
Repeating yourself causes twice as much work writing out the two definitions, twice as much work editing the definition in two places and causes the computer twice as much work doing the calculations twice. If you need a value, calculate it in one place and link this into the places where the calculation is needed. This is said another way in the DRY principle: "Every piece of knowledge must have a single, unambiguous, authoritative representation within a system." Your code will be faster to write, faster to edit and faster to calculate.
Work smarter
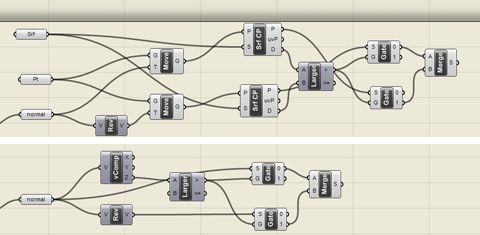
Above: original definition. Below: Using just the z component of the vector
Grasshopper encourages us to think about problems geometrically rather than computationally. Most of the time this is a good thing, but sometimes it can result in very inefficient code. A came across a great example of this the other week when a friend wanted to get the normals of a group of points on a surface and ensure the normals are always pointing upwards. For every point, he took the positive and negative normal, placed a point at the end and took the normal that put the point the furthest from the ground plane. This method is how we think about the problem geometrically, but is computationally slow because it involves creating points, projecting them and measuring distances. He asked me how to make it more efficient. I told him to take the normal for the point, check to see if the z-axis component is positive, if it is not then take the negative normal. This may not be an intuitive approach to the problem, but it is computationally efficient. Reconsidering a problem from a mathematical perspective can sometimes be rewarding.
Write your own functions
Writing your own functions can be very fickle, on some hardware configurations I have found rewriting Grasshopper nodes into C# or VB can greatly increase their execution time (sometimes as much as 10X). Other times it runs significantly slower. The following code finds the normal of the closest point on the surface. On my laptop this reduces the execution time from 400ms to about 100ms, however on my desktop it actually runs slower.
// Returns the normal of the surface at the closest point to the passed point.
private void RunScript(On3dPoint p, OnSurface s, ref object x, ref object y, ref object z)
{
double passS = 0;
double passT = 0;
s.GetClosestPoint(p, ref passS, ref passT);
RMA.OpenNURBS.On3dVector normal = s.NormalAt(passS, passT);
x = normal.x;
y = normal.y;
z = normal.z;
}
Write your own code
Grasshopper is pretty fast, but sometimes it just is not fast enough. You can either throw better hardware at the problem or better software at the problem. Writing your own C++/C#/VBA code can generate programs that run significantly faster than Grasshopper. The work done in Grasshopper is not lost though; it can act as a guide for structuring your new program, or as a specification to give a professional programmer.
Ruairi
Hey I thought with your interests in architectural computation that digital fabrication would be of interest to you also.
www.fabricate2011.org is a conference were running in London next year
We have a call for work with a a deadline in a month
Ruairi
Daniel
Hi Ruairi,
Thanks for the info about the conference. My supervisor, Mark Burry, is keynoting. I will take a look at the submission requirements.
Daniel