Cite as: Davis, Daniel, Jane Burry, and Mark Burry. 2011. “The Flexibility of Logic Programming.” In Circuit Bending, Breaking and Mending: Proceedings of the 16th International Conference on Computer Aided Architectural Design Research in Asia, ed. Christiane Herr, Ning Gu, Stanislav Roudavski, and Marc Schnabel, 29–38. Newcastle, Australia: The University of Newcastle.
Abstract
Flexibility is a major attribute of parametric modelling, however designers find it hard to maintain flexibility throughout their projects. One cause may be the programming paradigm of the parametric model. Currently this is dataflow programming, which makes it easy to create and flex parameters, but difficult to modify relationships. This paper investigates the implications of changing the programming paradigm in a parametric model to logic programming. A qualitative account is given of using dataflow programming and logic programming to generate a portion of the Sagrada Família church. It finds logic programming adept at translating explicit models into parametric models, but lacking continuous flexibility. This research demonstrates there are different types of flexibility within the model and architects can privilege certain flexibility types by selecting the programming paradigm of the model.
Keywords
Logic programming; parametric modelling; end user programming; practice based research.
1. Introduction
In a parametric model, the geometry is a function of a finite set of parameters, with the collection of relationships between functions and parameters sometimes termed the schema. If the schema does not contain a parameter to modify the model in the desired way, the schema needs to be modified in a process Woodbury (2010) describes as “erase, edit, relate and repair.” The process of relating and repairing the schema can be time consuming, particularly if the consequence of these modifications needs to be traced through a complex network of relationships. Mark Burry (1996) articulated one of the earliest instances of this problem in architectural practice, which occurred when he attempted to modify a schema of the Sagrada Família to generate paraboloids instead of conoids and concluded that there was “no solution other than to completely disassemble the model and restart at that critical decision.” Burry went on to suggest delaying the construction of the parametric model until the design problem is known, a practice that is common in contemporary architecture where parametric models are often not built until the design documentation stage. Constructing parametric models reveals “potential ranges of possibilities” and leads to further design exploration by design teams that, paradoxically, may not be accommodated in the schema of the model whose variability has suggested these new avenues. (Burry and Burry, 2006) The rigidity of parametric models to unanticipated design changes (a common occurrence in a cyclic design process) is a persistent problem that has not improved despite the now widespread use of parametric modelling in practice. Woodbury, Aish, and Kilian (2007) suggest that design changes can be anticipated through a series of ‘design patterns’ employed whilst constructing a parametric schema. Their work is significant for two reasons: firstly it suggests that parametric flexibility is related to the structure of the parametric schema; secondly it provides a model for improving parametric schema through appropriating software engineering principles from computer science.
In computer science, logic programming is one alternative to dataflow programming (the predominant software paradigm for parametric models). This paper investigates the affect on parametric models, in relation to their construction and modification, of changing the schema paradigm from a dataflow paradigm to a logic programming paradigm. The study gives a qualitative account of using the two paradigms to solve an actual design problem faced on Antonio Gaudí’s Sagrada Família church. The paper begins with the history of logic programming in architecture, followed by a description of the implementation method, and a discussion about using logic programming and dataflow programming to generate parametric schemas, before concluding with the findings of this study.
2. Schema Paradigms and Logic Programming in architecture
2. 1. The Dataflow Parametric Schema
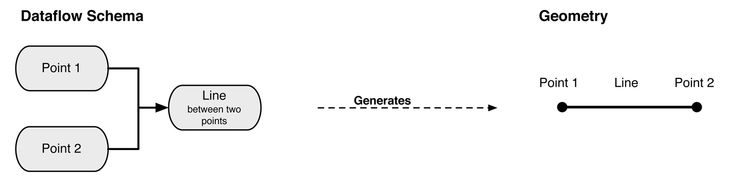
Figure 1 – Left: A schema as a directed acyclic graph. The data from the two points flows to the line node informing its construction. Right: Geometry that results from schema on left.
The parametric schema is the collection of relationships within a parametric model. The schema can be represented as a directed acyclic graph, where the connection between nodes represents a relationship in the parametric model (Figure 1). This graph is a type of dataflow programming where the nodes represent operations and the edges describe the flow of data between operations. Modifying the input data, changes the data that flows through the graph, in turn modifying the output (In Figure 1, if the location of Point 1 is modified, the line is automatically redrawn). Being able to automatically redraw geometry by only modifying input data is one of the advantages of parametric modelling and can be thought of as continuous flexibility.
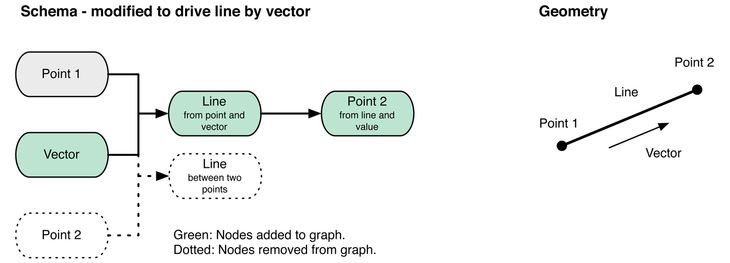
Figure 2 – Left: Modification of schema in Figure 1 so that the line follows a vector. Note that Point 1 is all that remains of the schema in Figure 1, even though the geometry on the right has not changed radically.
Parametric models generated with dataflow programming can become difficult to modify if the model lacks an input to change the geometry in the desired way. When this occurs, the schema must be manually rebuilt to accommodate the new input in a process Woodbury (2010) describes as “erase, edit, relate and repair.” The model’s ability to undergo this process can be described as discrete flexibility. In dataflow languages these processes can be problematic because relating and repairing relationships between nodes can change the flow of data with downstream consequences throughout the schema, even if the physical relationships between the geometry remains the same. Figure 2 shows adding a vector as an input to the schema in Figure 1 rearranges the relationships within the schema to the point where it would be easier to build the schema in Figure 2 from scratch than modify the schema in Figure 1. It is not uncommon for a complex production model to encounter these moments of discrete inflexibility, causing major time delays to the project while relationships are either reconstructed or the schema rebuilt from scratch (Burry and Burry, 2006).
2.2. Logic programming and background work
One alternative to dataflow programming is logic programming. Using logic programming, the user can focus on describing relationships between objects and leave the logical inferences (in this case the way data flows in these relationships) for the computer to deduce. Logic programming has been the subject of much investigation within architecture, beginning with Swinson’s 1982 paper Logic Programming: a computing tool for the architect of the future. Swinson utilised logic programming on four simple spatial planning problems and proposed this as an area for further investigation.
Following on from Swinson’s work, there was a flurry of studies in the mid 80’s through to the mid 90’s. In 1984 Gonzales et al concluded, incorrectly, that computers and CAD will be based on logic programming in the future. The first examples of logic programming used to draw 2d parametric shapes came in 1985 from Brüderlin, and in 1986 from Helm and Marriott. A more comprehensive attempt to generate 3D parametric models was made by Woodbury (1990) using the ACEND language – not strictly a logic programming language, although it shares many similarities. In the same year Mitchell (1990) released the Logic of Architecture, which contains descriptions of architecture in first order logic, similar to Prolog. The closest project to our project in technical implementation is Aldefeld’s (1988) use of forward-chaining to infer rules about constraints on parametric models. We use a similar method to infer rules about parametric schemata. A comprehensive review of logic programming in architecture between the mid 80’s through to the mid 90’s is documented in Fudos’ PhD thesis (1995).
In the late 90’s and 00’s, research into logic programming in architecture dropped off dramatically. Despite this, there are still examples of logic programming experiments, such as Martin and Martin’s Ployformes tool (1999) to draw complex polygons and Makris et al MultiCAD (2006), which combines logic programming with a genetic algorithms.
Despite the optimism of Swinson, logic programming has not become the “computing tool for the architect of the future” (Swinson, 1982). It is interesting to note that for all of their proclamations about the future of architecture, none of the papers surveyed applied logic programming to an architecture project. This case study differs from prior research by testing logic programming in a highly contained geometrical design problem from the Sagrada Família that exhibits the messy complexity, experienced in practice, of resolving multiple design constraints simultaneously. Unlike the previous research, which attempted to create the entire geometric model with logic programming, this research uniquely explores generating just the parametric schemata through logic programming and measures its success in relation to schema flexibility.
2.3. Logic Programming Applied To Parametric Schema
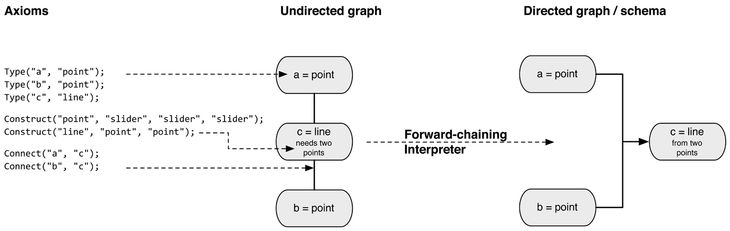
Figure 3 – How a parametric schema is constructed with logic programming. Progression from axioms, into an undirected graph, which is then interpreted into a schema.
Defined by Sterling and Shapiro (1994), logic programming has two parts: a set of axioms “defining relationships between objects” and an interpreter that “deducts the consequences” of the axioms. These steps correspond to our logic programming process (Figure 3) where initially axioms about the schema are declared, then in an intermediate step the axioms are compiled into an undirected graph, and then finally the interpreter infers the flow of data through the schema. The interpreter is based on a forward-chaining reasoning method. In Figure 3, the interpreter can be infer that Node A (a point) is the parent of Node C (a line) because the axioms declare that a line can be constructed from a point, and that a point cannot be constructed from a line. If the graph is over-constrained, the user is asked to resolve conflicts between the axioms. If the graph is under-constrained, a depth first search is applied to discover possible configurations for the user. Ideally the axioms will fully define the graph and the forward chaining interpreter will be able to infer the entire flow of data in the schema.
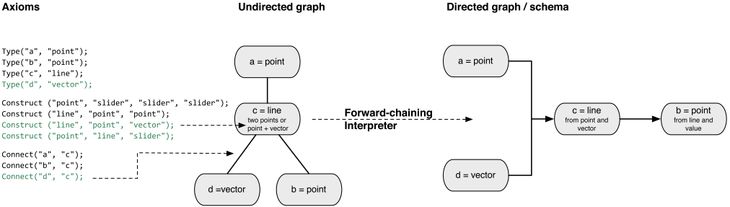
Figure 4 – Modification of the axioms from Figure 3 so that a vector drives the schema. This is the same modification as was seen in Figure 2. The text in green is additional axioms from Figure 3, the interpreter then automatically rebuilds the schema from these axioms.
The benefit of this method is that the user only needs to define connections between nodes, while the interpreter can infer the parent-child orientation of these relationships, generating the flow of data. Therefore, rather than “erase, edit, relate and repair” the user only needs to erase and edit the axioms, with the relating and repairing automatically deduced by the logical interpreter. Figure 4 shows adding a vector as an input to the schema in Figure 3 can be achieved by adding four new axioms while the interpreter infers the new dataflow (contrast this to the example in Figure 2, where, one the same problem, rebuilding the dataflow schema was easier than modifying it). This example depicts how the forward-chaining interpreter can carry out the stages of relating and repairing during a discrete modification of the schema, although this example also exposes how an additional layer of abstraction could make it difficult for the user to understand why interpreter has constructed particular relationships.
3. Application to the Sagrada Família
This section compares dataflow programming and logic programming as a method to solve a real constraint problem in the geometry for the ‘Fronton’ (gable) of the Sagrada Família.
3.1. The Problem faced on the Sagrada Família
The Sagrada Família by Antoni Gaudí’s has been under construction in Barcelona, Spain since 1882. Design and construction has recently commenced on the tower of Jesus; the central tower above the crossing. Forming the base of this tower are the ‘Frontons’ which are a matching set of 17 metre high arches placed above three windows on opposite sides of the tower. The Frontons were designed parametrically, however during the design process they were converted into explicit geometry and over subsequent revisions the original parametric properties became lost. In 2010, during the preparation of the construction documentation for the Frontons, it was decided the original parametric rules needed to be reapplied to the distorted geometry by converting it back into a parametric model. An example of the distortions is given in Figure 5.
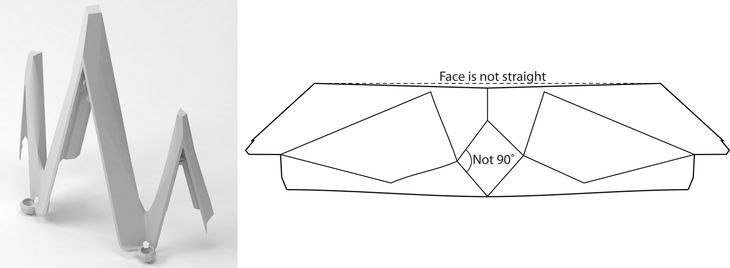
Figure 5 – Left: Final version of the Fronton produced by dataflow programming. Right: Plan view of Frontons illustrating two problems with the original model, faces that were not orthogonal and angles that were not correct – every face had one of these errors.
3.2. Using a Dataflow Schema
The conversion of the Frontons from an explicit model to a parametric model was initially undertaken using a dataflow parametric model. The process of generating the model occurred over a period of two weeks and took 32 hours. The final dataflow model was driven from 35 numeric parameters, which flowed through approximately 3000 connections to 1050 operations generating the revised geometry of the Frontons. The architects asked for two modifications, but fortunately the schema was developed with parameters anticipating these changes and the modifications occurred without rebuilding the schema.
3.3. Using a Logic Programming Schema
The same problem of converting the explicit model of the Frontons to a parametric model was solved with logic programming. Approximately 600 axioms were required to generate the schema. Most axioms could be automatically generated by a program that identified the geometric relationships already present in the explicit model (this can not be done on a graph based schema because they require not only the relationship, but the orientation of the relationship as well). The remaining 100 axioms were generated manually in a process that took 5 hours, making it significantly faster than dataflow programming. The two modifications could be accommodated by adding new axioms and this in turn allowed the forward-chaining algorithm to infer the modified schema.
4. Comparison and Discussion
4.1. Relative speed
It was approximately 5 times faster to build the schema with logic programming compared to dataflow programming. The increase in speed came from logic programming being able to generate large parts of the axioms automatically from the already existing, explicit, geometry of the Frontons. This speed advantage seems highly problem dependent and any problem that does not involve converting explicit geometry into a parametric model is unlikely generate such a speed difference.
4.2. Legibility
As the complexity of the schemas increased, both methods became illegible. In the dataflow language the connections were like spaghetti, making it difficult to track what rules had been applied; on three occasions rules were not applied because they seemed to be already present, a fact only uncovered by project architects measuring the model. Logic programming was equally difficult to read because it referred to geometry by name and it was difficult to assign meaningful names to the 111 points and 96 surfaces. This was slightly mitigated by grouping axioms together, so even if the axioms were illegible, the user could understand a group’s function. The extra layer of abstraction generated by using logic programming was not an issue in this case because the problem was so complex the only way to understand the system was through the output, in this case the geometry. Legibility is still a largely unexplored aspect of parametric modelling. It has implications for the use (and reuse) of parametric models in a team environment because editing the model requires comprehending it first. Neither dataflow programming nor logic programming addresses this issue, but modular programming or unit testing may offer fruitful areas of enquiry.
4.3. Flexibility
Flexibility is often described on a spectrum of more flexible and less flexible. Indeed the premise of this research was to discover a more flexible parametric modelling technique. However, more flexible is an insufficient description of the differences between logic programming and dataflow programming. Flexibility is not a spectrum, it is a combination of modelling attributes whose measurements is context dependent.
In the context of a real constraint problem in the geometry for the Fronton of the Sagrada Família: logic programming was the more flexible way to generate the schema from explicit geometry; both methods were equally flexible when making the required changes, although changes took significantly longer to propagate in logic programming; and both methods were equally illegible when identifying where to make the changes. However, this can not be extrapolated to all modelling situations because the results are highly dependent upon circumstance – such as there being pre-existing explicit geometry and the problem being of a high level of complexity. What can be extrapolated is the characteristic flexibility of the programming paradigm in each of these aspects – logic programming is likely to be more flexible than graph based modelling when converting explicit models to parametric models, and likewise, dataflow programming is likely to be more flexible when propagating parameter changes through the model. Since a parametric model cannot be easily switched from one programming paradigm to the other, the initial decision regarding what programming paradigm to generate the parametric model in, is critical. This is a decision can help make the model more or less flexible in particular aspects of flexibility. Further research is needed to help guide designers in making this decision.
4.4 Have we seen this before?
In many ways, the current situation with inflexible parametric models mirrors the 1960’s ‘software crisis’ where the major hindrance to the application of computation became the software developer’s ability to write code for these complex problems. In a similar way, the current limitation on parametric modelling is the designer’s ability to generate a flexible parametric model, particularly when faced with the complexity of pioneering projects like the Sagrada Família. There was no ‘silver bullet’ to the software crisis, instead new programming paradigms, new ways of structuring code, new code libraries, new environments for generating code and new ways of managing code development, helped pull programming out of its crisis (Brooks, 2010). This research has shown that the programming paradigm of the parametric model is one way to influence model flexibility, but there is still much more to learn from how software engineers structure code.
5. Conclusion
Logic programming is not a ‘silver bullet’ for parametric flexibility. Instead, this paper has shown that flexibility manifests in different forms within the parametric model, and that the programming paradigm of the model has some influence over these types of flexibility. By selecting the programming paradigm the designer can privilege certain types of flexibility, although how to make this decision deserves to be further explored. In this study, our novel application of logic programming to the generation of parametric schema, facilitated the translation of an explicit model into a parametric model while hindering the continuous flexibility of the model, when compared to a similar model created with dataflow programming. This paper has demonstrated that the programming paradigm has a significant impact on how long a parametric model takes to generate, as well as types of flexibility present.
Acknowledgements
This research was funded by the Australian Research Council Discovery Grant, Challenging the Inflexibility of the Flexible Digital Model, lead by Mark Burry (RMIT), John Frazer (QUT) and Jane Burry (RMIT). The work on the Sagrada Família was funded with the generous support of the Patronat of the Sagrada Família church.
References
Aldefeld, B.: 1988, Variation of geometries based on a geometric-reasoning method, Computer-Aided Design, 20(3), 177-126.
Brüderlin, B.: 1985, Using Prolog for Constructing Geometric Objects Defined by Constraints: Proceedings of EUROCAL ’85, Linz.
Brooks, F.: 2010, The Design of Design: Essays from a Computer Scientist, Pearson, Boston.
Burry, J. and Burry, M.: 2006, Sharing Hidden Power: Communicating latency in digital models: Proceedings of 24th eCAADe Conference, Education and research in Computer Aided Architectural Design in Europe, Volos.
Burry, M.: 1996, Parametric Design and the Sagrada Família, Architectural Research Quarterly, 1996(1), 70-80.
Fudos, I.: 1995, Constraint Solving for Computer Aided Design, PhD, Purdue University.
Gonzales, J.; Williams, M. and Aitchison, I.: 1984, Evaluation of the Effectiveness of Prolog for a CAD Application, IEEE Computer Graphics and Applications, 4(3), 67-75.
Helm, R., Marriott, K.: 1986, Declarative Graphics: Proceedings of 3rd International Conference on Logic Programming, Association for Logic Programming, London.
Makris, D.; Havoutis, I.; Miaoulis, G. and Plemenos, D.: 2006, MultiCAD – MOGA A System for Conceptual Style Design of Buildings: Proceedings of 3ia2006, International Conference on Computer Graphics and Artificial Intelligence, Limoges.
Martin, P. and Martin, D.: 1999, PolyFormes: Software for the declarative modelling of polyhedral, The Visual Computer, 15(2), 55-76.
Mitchell, W.: 1990, The Logic of Architecture, MIT Press, Massachusetts.
Sterling, L. and Shapiro, E.: 1994, The Art of Prolog, MIT Press, Massachusetts.
Swinson, P.: 1982, Logic Programming: A computing tool for the architect of the future, Computer-Aided Design, 14(2), 97-104.
Woodbury, R.: 1990, Variations in Solids: A declarative treatment, Computer and Graphics, 14(2), 173-188.
Woodbury, R.: 2010, Elements of Parametric design, Routledge, Oxford.
Woodbury, R.; Aish, R., and Kilian, A.: 2007, Some Patterns for Parametric Modeling: Proceedings of 27th ACADIA Conference, Association for Computer Aided Design in Architecture (ACADIA), Halifax.
Jose Hernandez
Daniel!
The content and form of this blog of your's is exquisite. I found through a related search on "the art of mathematics".
I love the layout and typesetting and wanted to ask if this is a custom WordPress theme.
Thank you for your posts - I've only read a few ... but your thesis and your illustrations on hyperbola construction are delighful.
Daniel
Hi Jose, thanks for you support! The theme is a custom WordPress design that I created, glad you enjoy it.